Elements of Statistical Inference, Part I
September 3, 2025
Statistical inference?
Statistics uses tools from probability and data analysis to
- draw inferences about populations from samples
- quantify uncertainty (or confidence) about an inference
We’ll illustrate inferential principles in the setting of
- estimating average characteristics of a well-defined population
- drawing conclusions about that characteristic
Perspectives on statistical inference
Some pithy philosophy on statistics
- Statisticians are “engaged in an exhausting but exhilarating struggle with the biggest challenge that philosophy makes to science: how do we translate information into knowledge?” –Senn (2022)
- “Statistics is the art of making numerical conjectures about puzzling questions.” –Freedman, Pisani, and Purves (2007)
- “Statistics is an area of science concerned with the extraction of information from numerical data and its use in making inferences about a population from which the data are obtained.” –Mendenhall, Beaver, and Beaver (2012)
- “The objective of statistics is to make inferences (predictions, decisions) about a population based on information contained in a sample.” –Mendenhall, Beaver, and Beaver (2012)
Example: The YRBSS survey data
Consider the Youth Risk Factor Behavior Surveillance System (YRBSS), a survey conducted by the CDC to measure health-related activity in high school aged youth. The YRBSS data contain
- 2.6 million high school students, who participated between 1991 and 2013 across more than 1,100 separate surveys.
- Dataset
yrbssin theoibiostatRpackage contains the responses from the 13,583 participants from the year 2013.
The CDC used 13,572 students’ responses to estimate health behaviors in a target population: 21.2 million high school-aged students in US in 2013.
Of populations and parameters
The mean weight among the 21.2 million students is an example of a population parameter, i.e.,
The mean within a sample (e.g., as with the 13,572 students in YRBSS), is a point estimate
Estimating the population mean weight from the sample of 13,572 participants is an example of statistical inference.
Why inference? It is too tedious to gather this information for all 21.2 million students—also, it is unnecessary.
Of populations and parameters
In nearly all studies, there is one target population and one sample.
Suppose a different random sample (of the same size) were taken from the same population—different participants, different
Sampling variability describes the degree to which a point estimate varies from sample to sample (assuming fixed sampling scheme).
Properties of sampling variability (randomness) allow for us to account for its effect on estimates based on a sample.
Sampling from a population
- The exact values of population parameters are unknown.
- To what degree does sampling variability affect
- As an example, let the YRBSS data (of 13,572 individuals) be the target population, with mean weight
- Sample from this population (e.g.,
- How well does
- Sample from this population (e.g.,
- Take many samples to construct the sampling distribution of
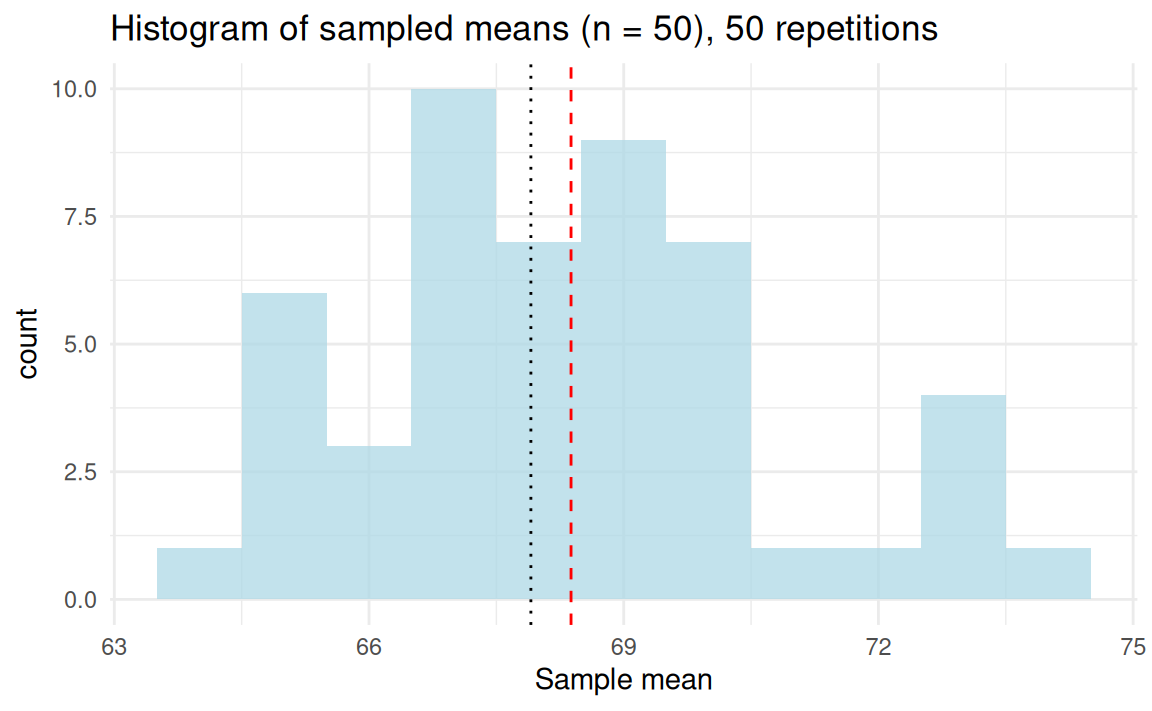
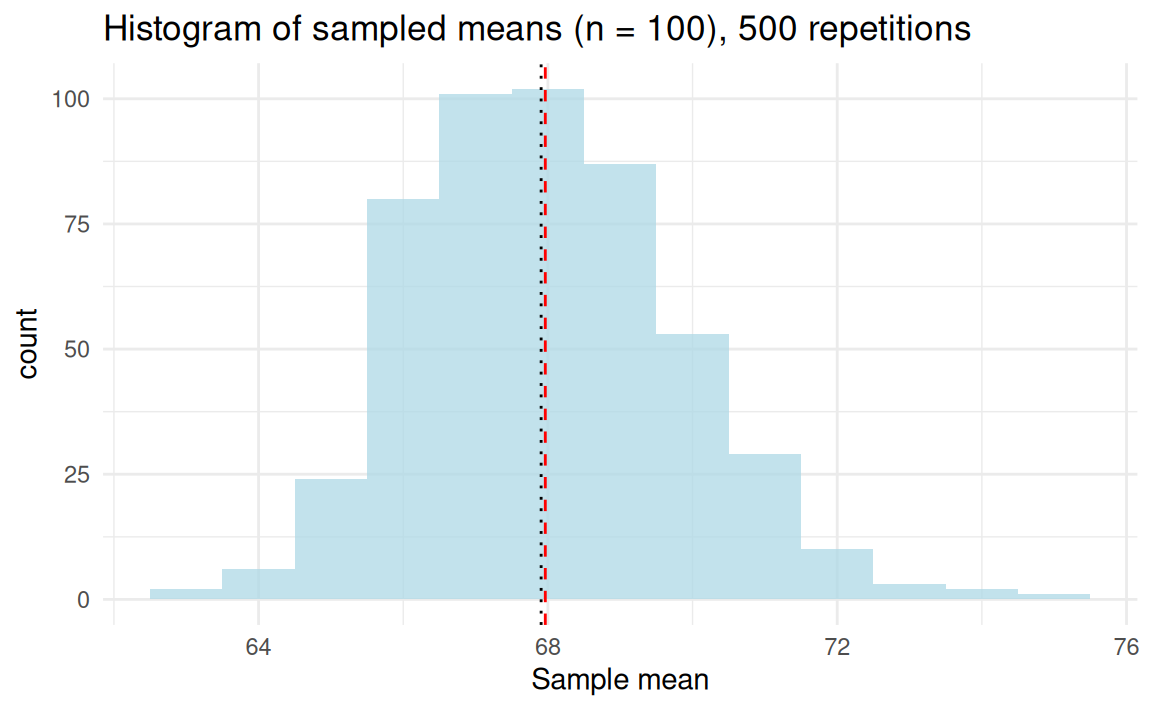
Taking samples from the YRBSS data
The estimator
The sample mean as a random variable
The statistic
- The sampling distribution of
- The variability of
Any sample statistic is a random variable since each sample drawn from the population ought to be different.
When the data have not yet been observed, the statistic, like the corresponding RV, is a function of the same random elements.
The standard error of
If
The variability of a sample mean decreases as sample size increases:
- Typically,
- The term
Leveraging variability: Confidence intervals
A confidence interval gives a plausible range of values for the population parameter, coupling an estimate and a margin of error:
Confidence intervals: Definition and construction
A confidence interval with coverage rate
Since
Confidence intervals: The fine print…
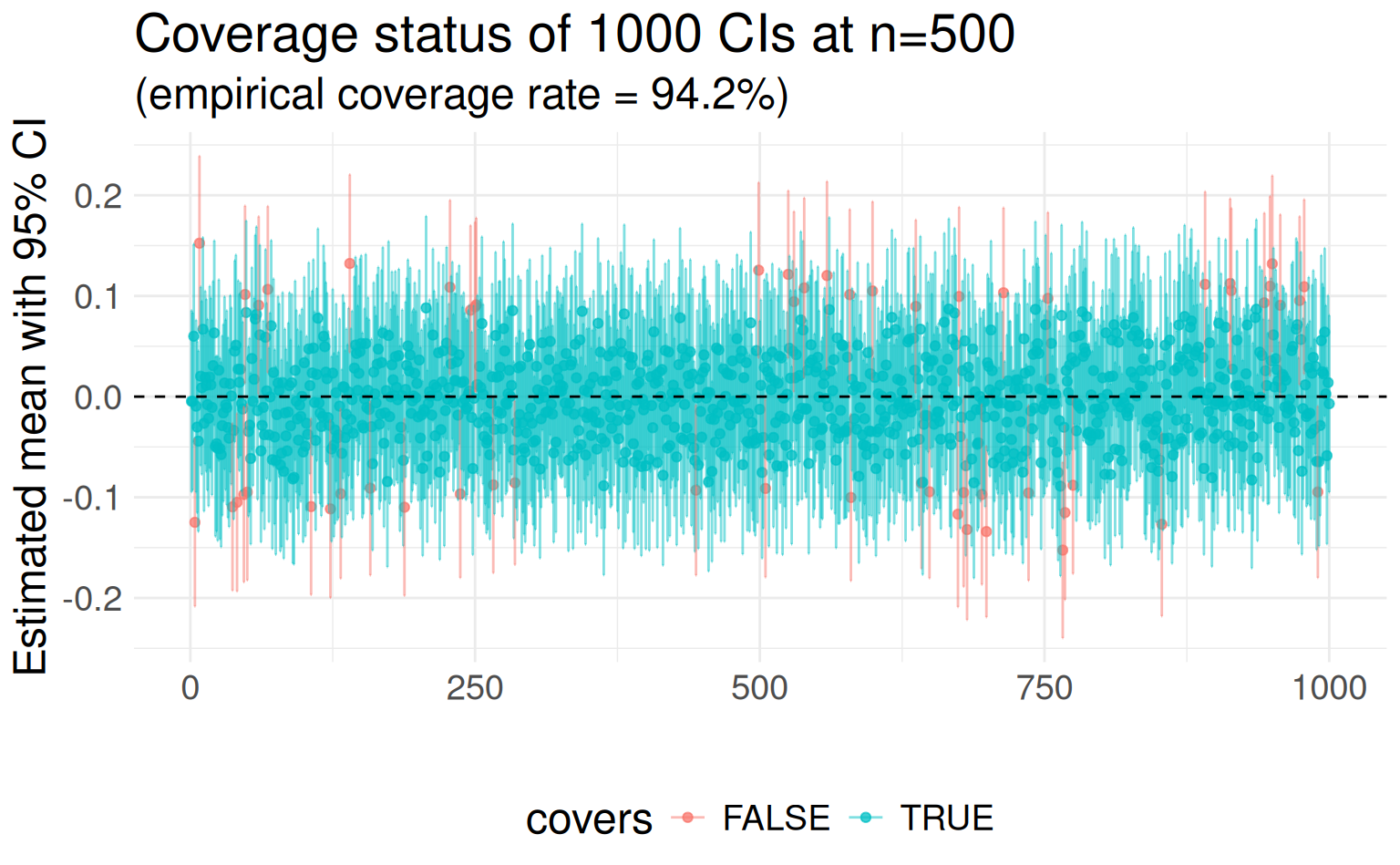
The confidence level may also be called the confidence coefficient. Confidence intervals have a nuanced interpretation:
- The method for computing a 95% confidence interval produces a random interval that—on average—contains the true (target) population parameter 95 times out of 100.
- 5 out of 100 will be incorrect, but, of course, a data analyst (or reader of your paper!) cannot know whether a particular interval contains the true population parameter.
- The data used to calculate the confidence interval are from a random sample taken from a well-defined target population.
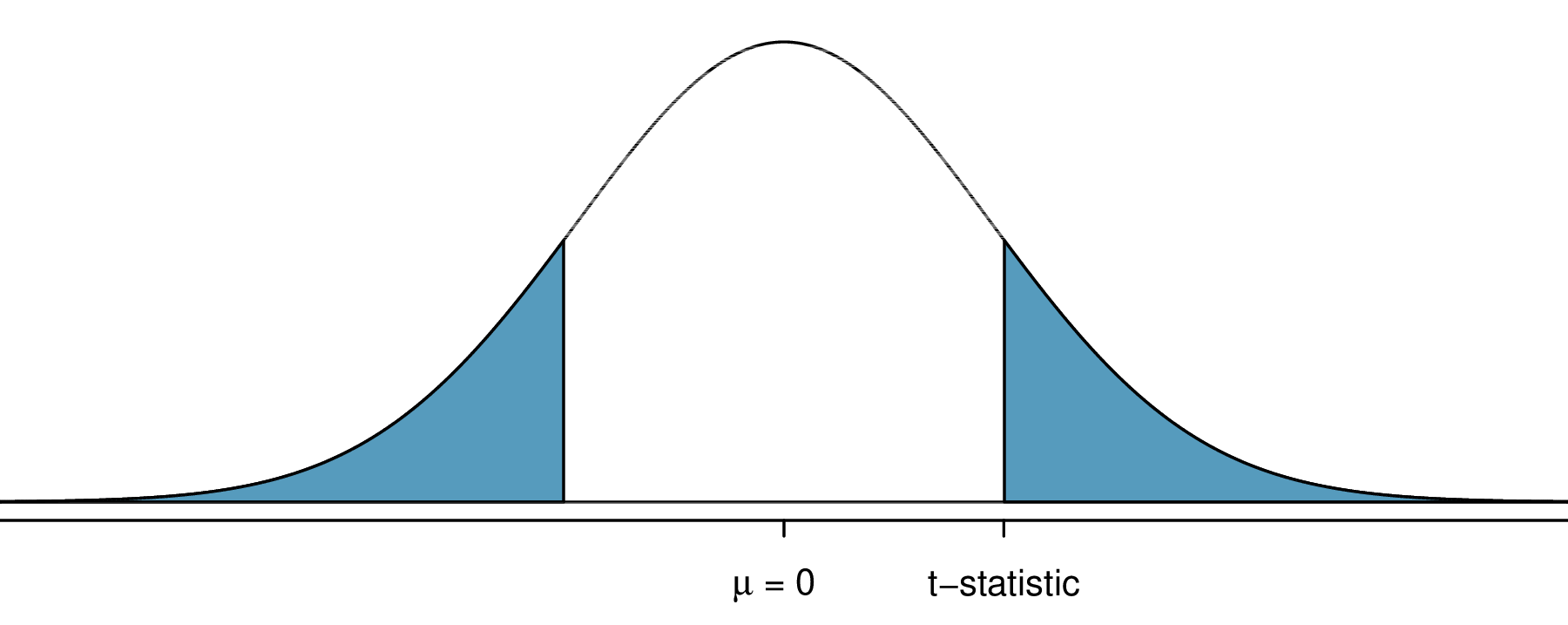
Confidence intervals: Proof by picture
Asymptotic
Random interval
The
The
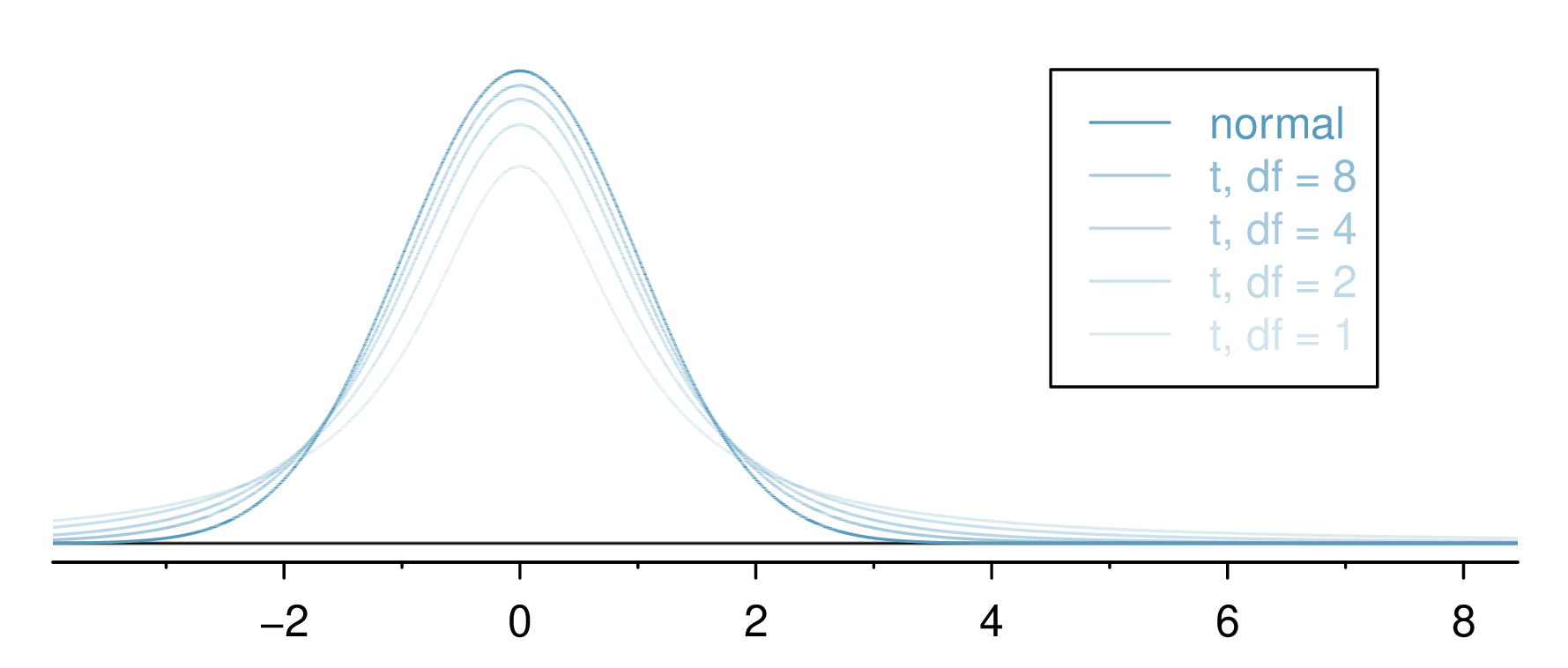
It has an additional parameter–degrees of freedom (
- Degrees of freedom (
- The
- When
The
A (
A (
For a 95% CI, find
Calculating the critical
The R function qt(p, df) finds the quantile of a
Just let
Rdo the work for you…95% CI fromt.test():
Inference: Testing a hypothesis
Question: Do Americans tend to be overweight?
- Body mass index (BMI) is a scale used to assess weight status, adjusting for height.
- The CDC’s National Health and Nutrition Examination Survey (NHANES) assesses health and nutritional status of adults, children in the US.
| Category | BMI range |
|---|---|
| Underweight | |
| Healthy weight | 18.5-24.99 |
| Overweight | |
| Obese |
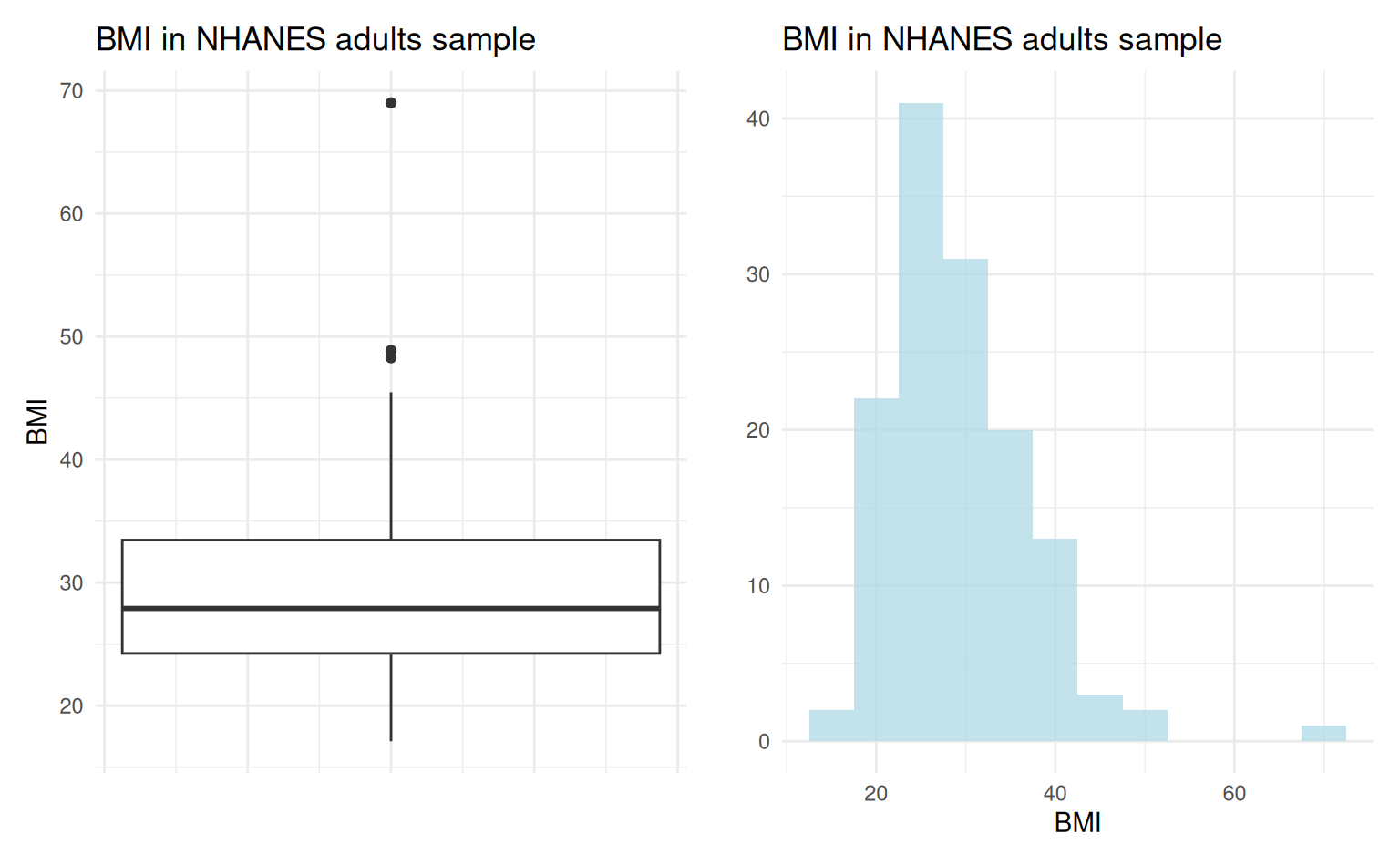
The NHANES sample
Can we use a 95% confidence interval? Yes!
Confidence interval suggests that population average BMI is well outside the range defined as healthy (BMI of 18.5-24.99):
[1] 27.81388 30.38524
attr(,"conf.level")
[1] 0.95If a (
- the observed data contradict the null hypothesis
- the implied two-sided alternative hypothesis is
Null and alternative hypotheses
- The null hypothesis (
- The alternative hypothesis (
- Since
- A hypothesis test evaluates whether there is evidence against
Framing null and alternative hypotheses
For our BMI inquiry, there are a few possible choices for
The form of
The choice of one- or two-sided alternative is context-dependent and should be driven by the motivating scientific question.
What’s “real”? The significance level
The significance level
In other words, it is a bar for the degree of evidence necessary for a difference to be considered as “real” (or significant)1 2.
In the context of decision errors,
Choose (and calculate) a test statistic
The test statistic measures the discrepancy between the observed data and what would be expected if the null hypothesis were true.
When testing hypotheses about a mean, a valid test statistic is
The devil is in the details
We will go on to talk about a few more practical versions of the
In each of these cases, some assumptions are required…
- measurements being compared (e.g., BMI) are randomly (iid) sampled from a normal distribution
- same unknown mean, same unknown variance (plus normality)
Justifying your assumptions is the hardest part
Given the context of your scientific problem, are these assumptions true or reasonable?
Calculate a
What is the probability that we would observe a result as or more extreme than the observed sample value, if the null hypothesis is true? This probability is the
- Calculate the
- A result is considered unusual (or statistically significant) if its associated
Quantifying surprise – the
Despite their popularity,
The surprisal value
The
The
For a two-sided alternative,
The
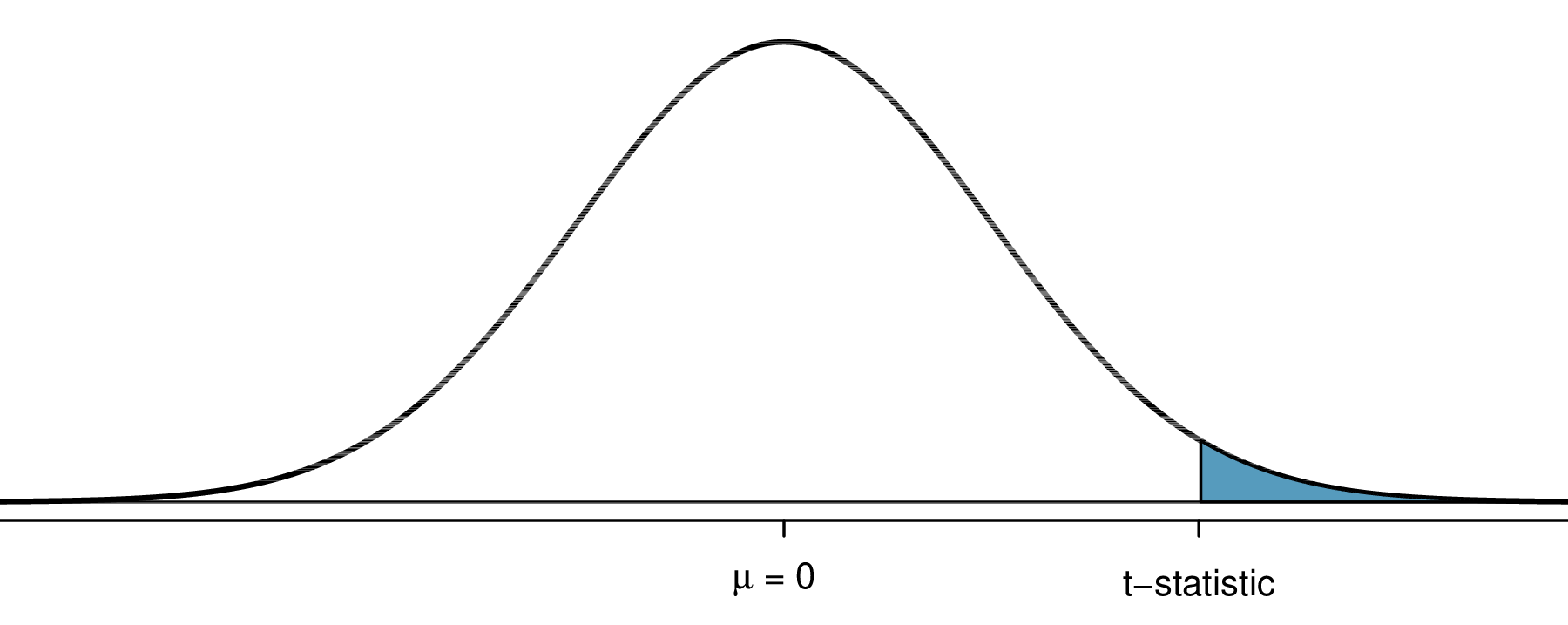
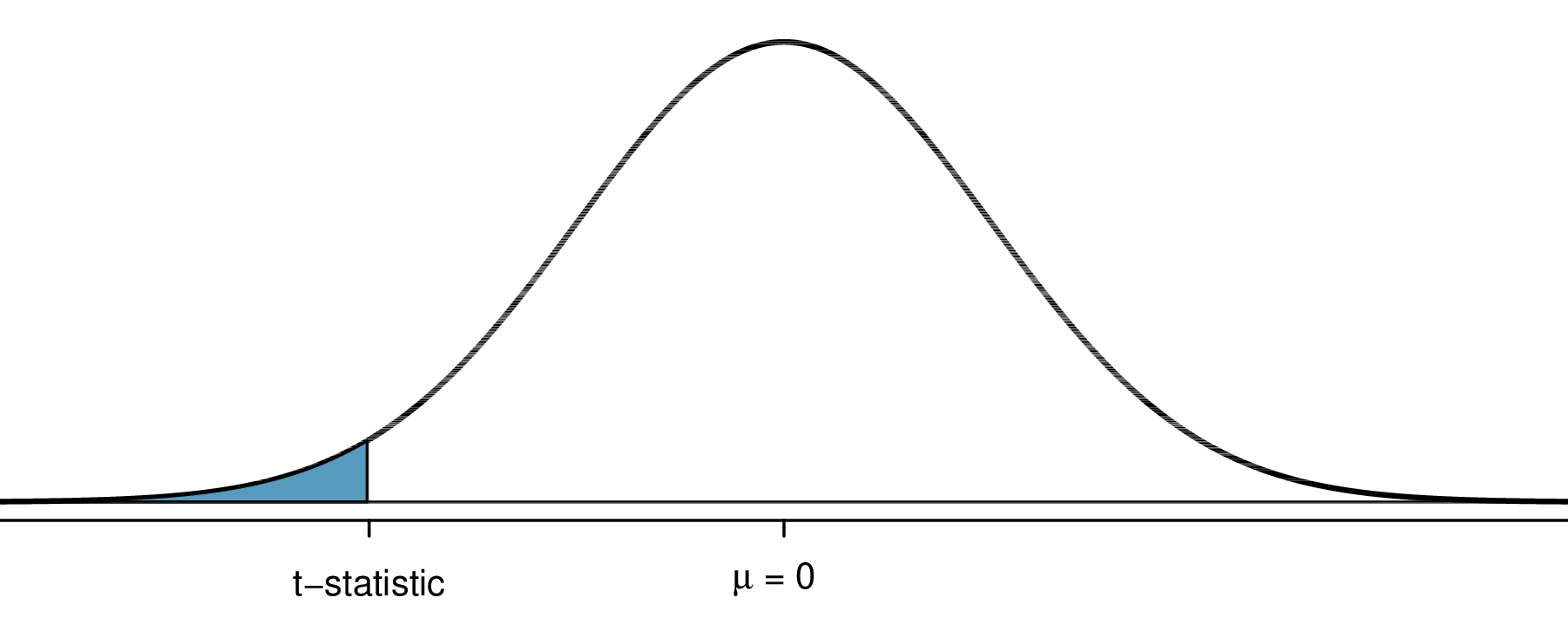
For a one-sided alternative, the
The
The smaller the
- If the
- If the
Always state conclusions in the context of the research problem.
Evaluating BMI in the NHANES adult sample
Question: Do Americans tend to be overweight?
One Sample t-test
data: nhanes.samp.adult$BMI
t = 11.383, df = 134, p-value < 2.2e-16
alternative hypothesis: true mean is greater than 21.7
95 percent confidence interval:
28.02288 Inf
sample estimates:
mean of x
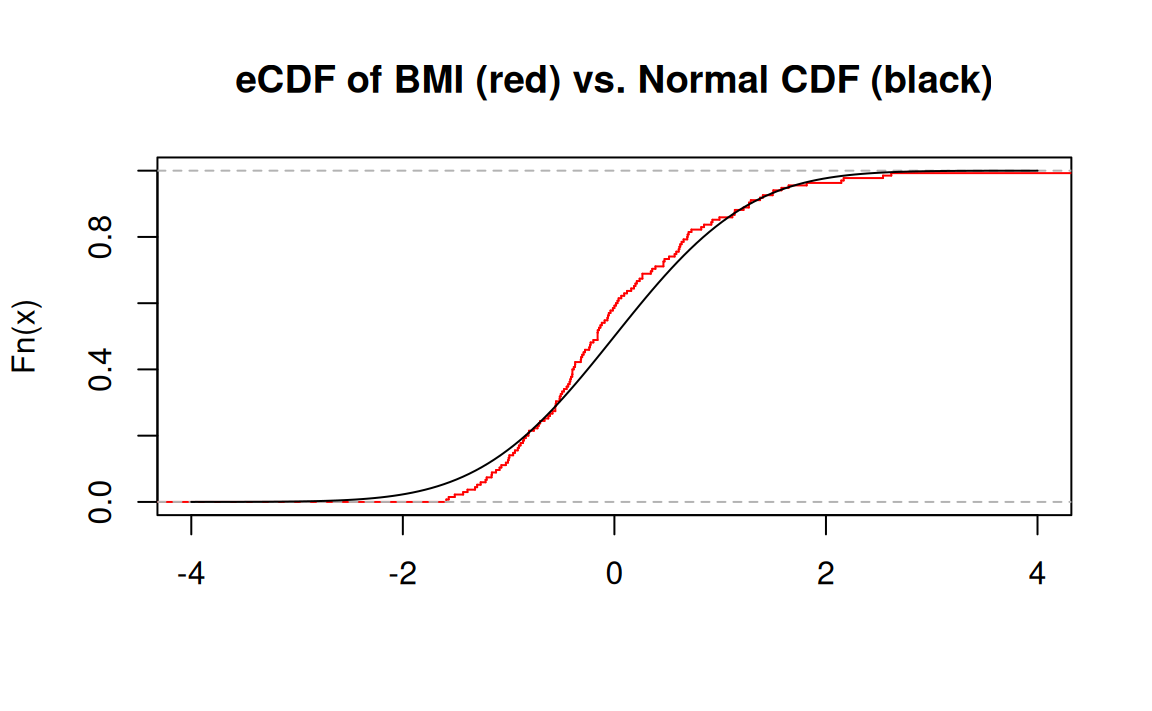
29.09956 The Kolmogorov-Smirnov (KS) test
The KS test is a nonparametric test that evaluates the equality of two distributions (n.b., different from testing mean differences).
The empirical cumulative distribution function (eCDF) is
The KS test uses as its test statistic
Using the KS test: Is BMI normally distributed?
References

HST 190: Introduction to Biostatistics